kutamaya

The golden ratio, also known as the divine proportion, golden mean, or golden section, is a number often encountered when taking the ratios of distances in simple geometric figures such as the pentagon, pentagram, decagon and dodecahedron. It is denoted , or sometimes .

The designations “phi” (for the golden ratio conjugate ) and “Phi” (for the larger quantity ) are sometimes also used (Knott), although this usage is not necessarily recommended.

The term “golden section” (in German, goldener Schnitt or der goldene Schnitt) seems to first have been used by Martin Ohm in the 1835 2nd edition of his textbook Die Reine Elementar-Mathematik (Livio 2002, p. 6). The first known use of this term in English is in James Sulley’s 1875 article on aesthetics in the 9th edition of the Encyclopedia Britannica. is an abbreviation of the Greek tome, meaning “to cut.” (”phi”) was apparently first used by Mark Barr at the beginning of the 20th century in commemoration of the Greek sculptor Phidias (ca. 490-430 BC), who a number of art historians claim made extensive use of the golden ratio in his works (Livio 2002, pp. 5-6). Similarly, the alternate notation The symbol

In the Season 1 episode “Sabotage” (2005) of the television crime drama NUMB3RS, math genius Charlie Eppes mentions that the golden ratio is found in the pyramids of Giza and the Parthenon at Athens. Similarly, the character Robert Langdon in the novel The Da Vinci Code makes similar such statements (Brown 2003, pp. 93-95). However, claims of the significance of the golden ratio appearing prominently in art, architecture, sculpture, anatomy, etc., tend to be greatly exaggerated.

has surprising connections with continued fractions and the Euclidean algorithm for computing the greatest common divisor of two integers.

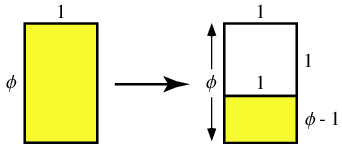
Given a rectangle having sides in the ratio , is defined as the unique number (i.e., such that the yellow rectangles shown above are similar). Such a rectangle is called a golden rectangle, and successive points dividing a golden rectangle into squares lie on a logarithmic spiral, giving a figure known as a whirling square. such that partitioning the original rectangle into a square and new rectangle as illustrated above results in a new rectangle which also has sides in the ratio

Based on the above definition, it can immediately be seen that

(1)

giving

(2)

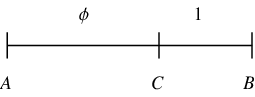
Euclid ca. 300 BC gave an equivalent definition of by defining it in terms of the so-called “extreme and mean ratios” on a line segment, i.e., such that

(3)

for the line segment illustrated above (Livio 2002, pp. 3-4). Plugging in,

(4)

and clearing denominators gives

(5)

which is exactly the same formula obtained above (and incidentally means that is a algebraic number of degree 2.) Using the quadratic equation and taking the positive sign (since the figure is defined so that 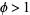1" border="0" height="14" width="31">) gives the exact value of , namely

			(6)
			(7)
			(8)

(Sloane’s A001622).

In an apparent blatant misunderstanding of the difference between an exact quantity and an approximation, the character Robert Langdon in the novel The Da Vinci Code incorrectly defines the golden ratio to be exactly 1.618 (Brown 2003, pp. 93-95).

The legs of a golden triangle (an isosceles triangle with a vertex angle of ) are in a golden ratio to its base and, in fact, this was the method used by Pythagoras to construct . The ratio of the circumradius to the length of the side of a decagon is also ,

(9)

Bisecting a (schematic) Gaullist cross also gives a golden ratio (Gardner 1961, p. 102).

Exact trigonometric formulas for include

			(10)
			(11)
			(12)

The golden ratio is given by the infinite series

(13)

(B. Roselle). Another fascinating connection with the Fibonacci numbers is given by the infinite series

(14)

A representation in terms of a nested radical is

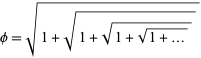(15)

(Livio 2002, p. 83).

is the “most” irrational number because it has a continued fraction representation

(16)

(Sloane’s A000012; Williams 1979, p. 52; Steinhaus 1999, p. 45; Livio 2002, p. 84). This means that the convergents are given by the quadratic recurrence equation

(17)

with , which has solution

(18)

where is the th Fibonacci number. This gives the first few convergents as 1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, … (Sloane’s A000045 and A000045), which are good to 0, 0, 0, 1, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 5, … (Sloane’s A114540) decimal digits, respectively.

As a result,

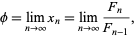infty)x_n=lim_(n->infty)(F_n)/(F_(n-1)), " border="0" height="37" width="136">

(19)

as first proved by Scottish mathematician Robert Simson in 1753 (Wells 1986, p. 62; Livio 2002, p. 101).

The golden ratio also satisfies the recurrence relation

(20)

Taking gives the special case

(21)

Treating (20) as a linear recurrence equation

(22)

in , setting and , and solving gives

(23)

as expected. The powers of the golden ratio also satisfy

(24)

where is a Fibonacci number (Wells 1986, p. 39).

The sine of certain complex numbers involving gives particularly simple answers, for example

			(25)
			(26)

(D. Hoey, pers. comm.). A curious (although not particularly useful) approximation due to D. Barron is given by

(27)

where is Catalan’s constant and is the Euler-Mascheroni constant, which is good to two digits.

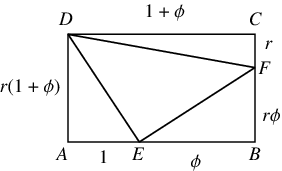
In the figure above, three triangles can be inscribed in the rectangle of arbitrary aspect ratio such that the three right triangles have equal areas by dividing and in the golden ratio. Then

			(28)
			(29)
			(30)

which are all equal.

The substitution map

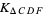	" border="0" height="14" width="12">		(31)
	" border="0" height="14" width="12">		(32)

gives

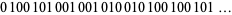01->010->01001->..., " border="0" height="14" width="171">

(33)

giving rise to the sequence

(34)

(Sloane’s A003849). Here, the zeros occur at positions 1, 3, 4, 6, 8, 9, 11, 12, … (Sloane’s A000201), and the ones occur at positions 2, 5, 7, 10, 13, 15, 18, … (Sloane’s A001950). These are complementary Beatty sequences generated by . This sequence also has many connections with the Fibonacci numbers. It is plotted above (mod 2) as a recurrence plot. and

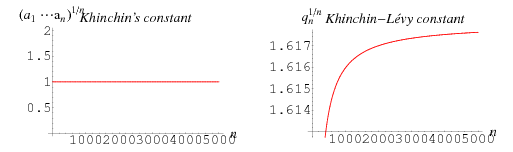
Let the continued fraction of be denoted and let the denominators of the convergents be denoted , , …, . As can be seen from the plots above, the regularity in the continued fraction of means that is one of a set of numbers of measure 0 whose continued fraction sequences do not converge to the Khinchin constant or the Khinchin-Lévy constant.

The golden ratio has Engel expansion 1, 2, 5, 6, 13, 16, 16, 38, 48, 58, 104, … (Sloane’s A028259).

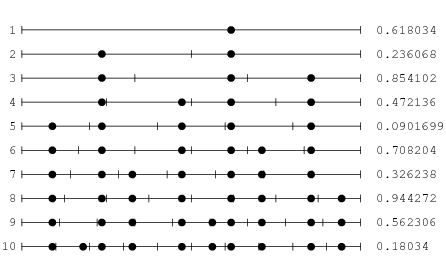
Steinhaus (1983, pp. 48-49) considers the distribution of the fractional parts of in the intervals bounded by 0, , , …, , 1, and notes that they are much more uniformly distributed than would be expected due to chance (i.e., is close to an equidistributed sequence). In particular, the number of empty intervals for , 2, …, are a mere 0, 0, 0, 0, 0, 0, 1, 0, 2, 0, 1, 1, 0, 2, 2, … (Sloane’s A036414). The values of for which no bins are left blank are then given by 1, 2, 3, 4, 5, 6, 8, 10, 13, 16, 21, 34, 55, 89, 144, … (Sloane’s A036415). Steinhaus (1983) remarks that the highly uniform distribution has its roots in the continued fraction for .

The sequence , of power fractional parts, where is the fractional part, is equidistributed for almost all real numbers 1" border="0" height="14" width="30">, with the golden ratio being one exception.

Salem showed that the set of Pisot numbers is closed, with the smallest accumulation point of the set (Le Lionnais 1983). [ dagdigdug ]